WisFaq!

De digitale vraagbaak voor het wiskundeonderwijs

HOME

samengevat

\require{AMSmath}

Hogere orde voorwaarden

Vraagstuk over mensen die naar kobalt zoeken in de grond en het meeste kobalt op een plek dat men kan vinden is x2 y. men zoekt een op een halve cirkel met diameter 2√3 met als middelpunt het nulpunt en als uiteinde het kamp.

Wat is de plek waar men het meeste kobalt in de grond kan vinden? Doe dit met de eerste orde voorwaarde en de tweede orde voorwaarde.

beste ik snap niet zo goed wat je hier moet doen wie kan me helpen?
poled
Student universiteit België - zondag 27 augustus 2023

Antwoord

Zo te zien gaat het om dit gebied:

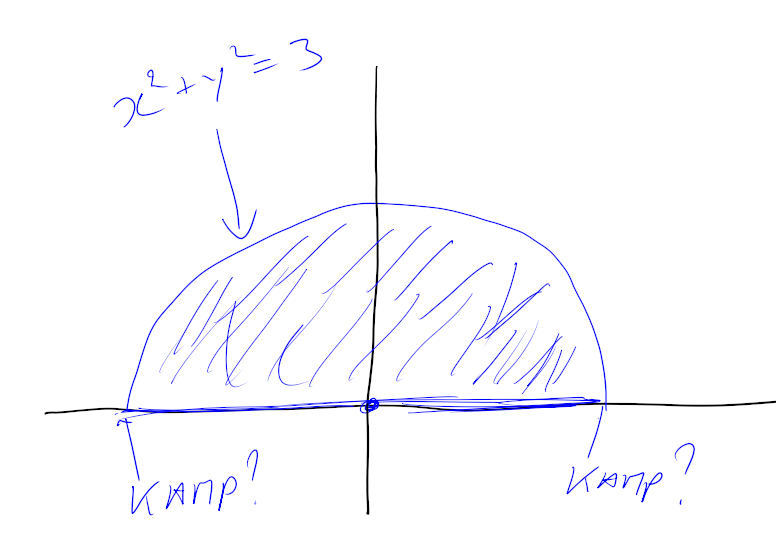
Diameter $2\sqrt3$ betekent straal $\sqrt3$, dus de vergelijking van de cirkel is $x^2+y^2=3$.
Ik vermoed dat het gaat om de functie gegeven door $f(x,y)=x^2y$.
Binnen dat gebied heeft $f$ geen stationaire punten, dus het maximum komt op de rand voor, en niet op de $x$-as want $f(x,0)=0$ voor alle $x$.
Ik zie twee manieren om het maximum op de rand op te sporen; ik weet niet of die in jouw boek eerst-orde en tweede-orde heten.

1. In de uitdrukking $x^2y$ kun je $x^2$ vervangen door $3-y^2$. Dan moet je dus het maximum van $g(y)=3y-y^3$ op het interval $[0,\sqrt3]$ bepalen.

2. Je gebruikt de multiplicatorenmethode van Euler en Lagrange: bepaal de stationaire punten van $x^2y-\lambda(x^2+y^2-3)$.
Dat geeft drie vergelijkingen:

$2xy-2\lambda x=0$
$x^2-2\lambda y=0$
$x^2+y^2-3=0$

De eerste vergelijking geeft $x=0$ of $\lambda=y$. De eerste mogelijkheid geeft $f(0,\sqrt3)=0$ en dat is geen maximum.
Via $\lambda=y$ vind je $x^2-2y^2=0$, gecombineerd met $x^2+y^2=3$ geeft dat het punt waar het maximum zit.

kphart

Vragen naar aanleiding van dit antwoord? Klik rechts..!
dinsdag 29 augustus 2023