WisFaq!

De digitale vraagbaak voor het wiskundeonderwijs

HOME

samengevat

\require{AMSmath}

Snijpunten van twee cirkels

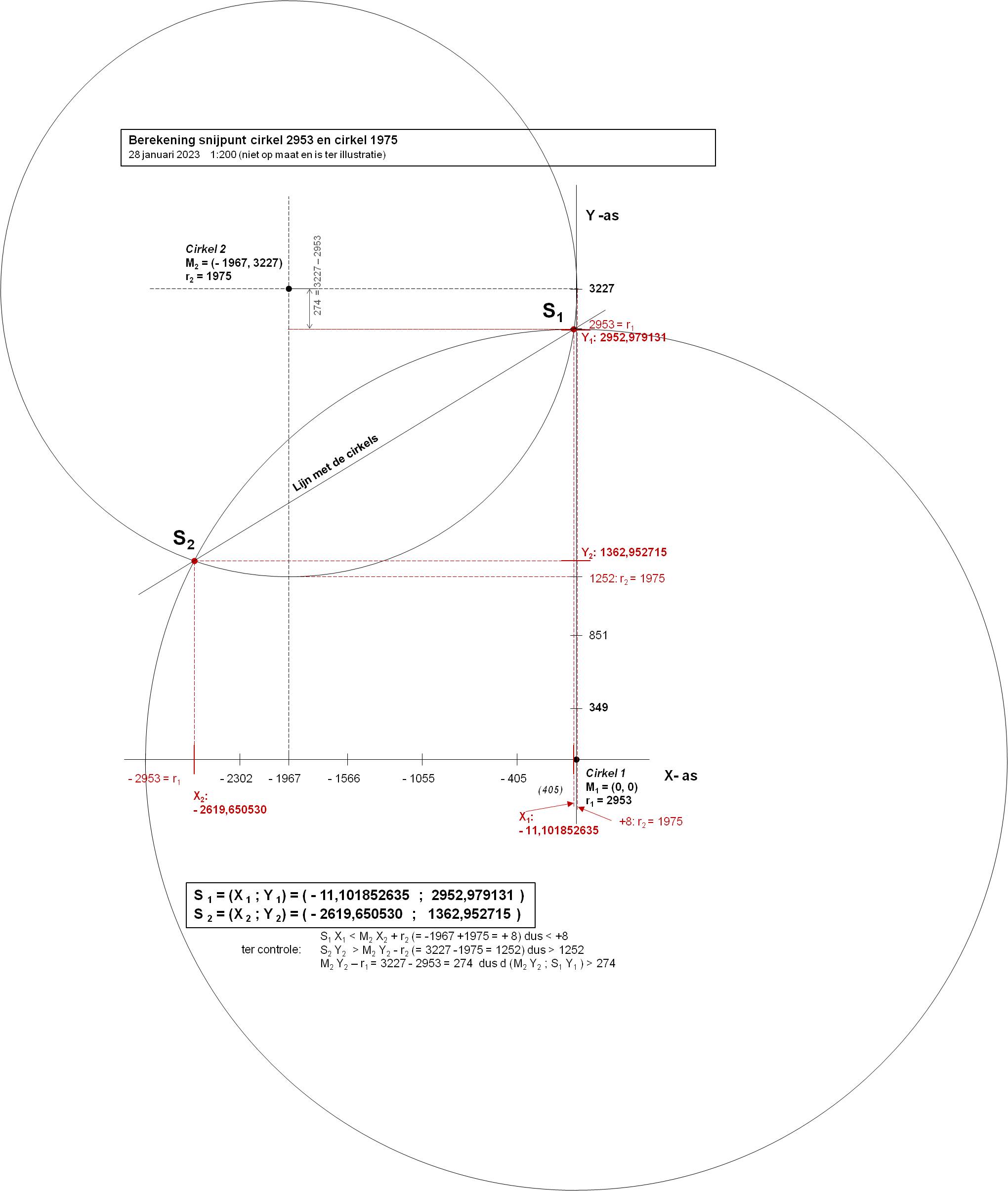
hierbij de situatieschets bij mijn vraag:

Ik ben snijpunten van twee cirkels aan het berekenen. Hierbij doe ik iets fout. Ik zie alleen niet waar en wat ik daar verkeerd doe. Ik kom uit op x² + 2630,752383x + 29082,97414 = 0 wat ik moet factoriseren, maar a.h.v. mijn tekening weet ik dat de SOM min 2630,752383x moet zijn.

Ik heb nu een aantal keren het proces doorlopen en volgens mij doe ik dat allemaal goed, maar zodra ik bij de formule uitkom waarmee ik de X-coördinaten van de twee snijpunten moet gaan bepalen blijkt dat ik structureel iets verkeerd doe met de min-tekens.
Boeken en internet bieden helaas geen oplossing.

Is het mogelijk dat u mijn berekening nakijkt?

De situatieschets (X-as en Y-as met de twee cirkels) en mijn berekening zal ik toevoegen.

Alvast vriendelijk bedankt.
Emmy
Emmy M
Iets anders - vrijdag 3 februari 2023

Antwoord

Ik heb de snijpunten met behulp van Maple bepaald:

De uitkomsten komen overeen met de jouwe.

De som van de $x$-coördinaten, $x_1+x_2$, is inderdaad $-2630{,}752383$. Er geldt in het algemeen dat als $x_1$ en $x_2$ oplossingen van een tweedegraadsvergelijking zijn, die vergelijking te schrijven is als $(x-x_1)(x-x_2)=0$, ofwel $x^2-(x_1+x_2)x+x_1x_2=0$.
Dat klopt voor jouw vergelijking: $-(x_1+x_2)=-(-2630{,}752383)=2630{,}752383$.

kphart

Vragen naar aanleiding van dit antwoord? Klik rechts..!
vrijdag 3 februari 2023