|
|
|
\require{AMSmath}
Grafiek van derdegraads functie vinden
Ik zit vast bij de volgende oefening:
Gegeven: 4 functievoorschriften, nl.:
- y= 1 - (x-2)3
- y= 1 + (x-2)3
- y= 2 - (x-1)3
- y= 2 + (x-1)3
Gevraagd: Welk van deze grafieken stelt de functie y= 1 + (x-2)3 voor?
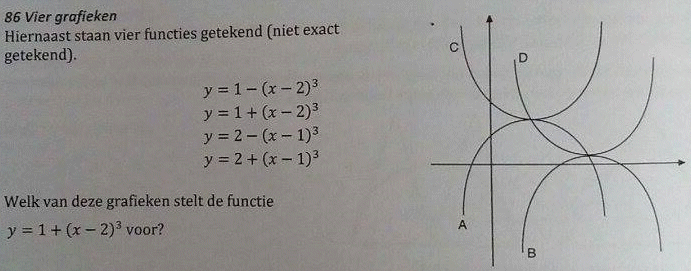
Ik heb eerst de afgeleide gezocht van de gevraagde vergelijking, hiermee kwam ik uit dat de grafiek een min heeft in x=2. Het is dus zeker een holle grafiek en geen convexe. Daarna heb ik y= 2 + (x-1)3 ook afgeleiden om te zien waar het min zich hier bevindt, het min is in dit geval in x=1, wat dus wil zeggen dat deze grafiek dichter tegen de y-as staat dan de eerste, waardoor ik op D kwam. Het antwoord is echter B... Weet u waarom?
Alvast bedankt voor de hulp
MinYoo
3de graad ASO - vrijdag 30 juni 2017
Antwoord
Beschouw y=1+(x-2)3 als een transformatie van de standaardgrafiek y=x3.
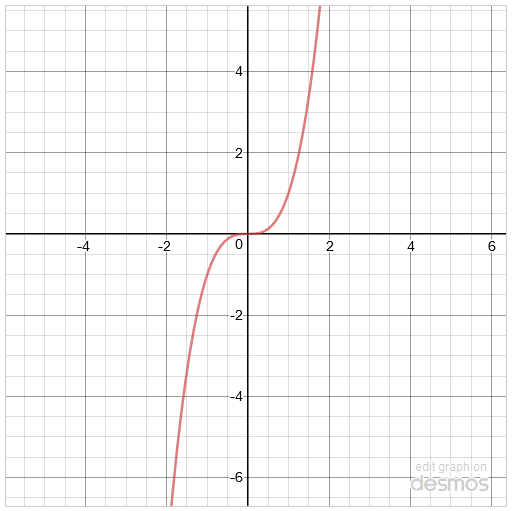
De grafiek is 2 naar rechts verschoven en 1 omhoog. Dus B.
|
Vragen naar aanleiding van dit antwoord? Klik rechts..!
vrijdag 30 juni 2017
|
|
home |
vandaag |
bijzonder |
gastenboek |
statistieken |
wie is wie? |
verhalen |
colofon
©2001-2024 WisFaq - versie 3
|
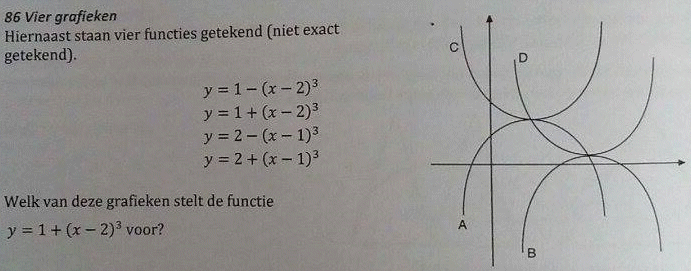
Re: Grafiek van derdegraadse functie vinden