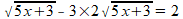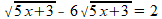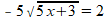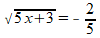WisFaq!

De digitale vraagbaak voor het wiskundeonderwijs

HOME

samengevat

\require{AMSmath}

Rekenen met wortel

Ik snap dit niet helemaal.

Wortel (5x +3) - 3 · 2 wortel (5x +3) = 2
Waarom wordt dit het volgende?
(5x + 3) - 3 · 2(5x +3) = 2 wortel (5x + 3)

Nu vermenigvuldig ik links bijna alles met de wortel behalve -3. Waarom moet je -3 ook niet met de wortel vermenigvuldigen? Ik dacht dat je alles wat je links doet rechts ook moet doen.
Gerard
Leerling bovenbouw havo-vwo - dinsdag 20 juni 2017

Antwoord

Hallo Gerard,

Als ik het goed begrijp, gaat het om deze vergelijking:

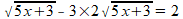
Je mag links en rechts van het is-gelijk-teken met √(5x+3) vermenigvuldigen. Het idee hierachter is: als links en rechts vóór vermenigvuldiging gelijk zijn, en je maakt beide √(5x+3) keer zo groot, dan zijn links en rechts ná vermenigvuldiging ook weer gelijk.

Om links √(5x+3) keer zo groot te maken, moet je elke term met deze wortel vermenigvuldigen, d.w.z.: alle 'dingen' die je bij elkaar optelt of van elkaar aftrekt. Links staan twee termen: de eerste term is √(5x+3), de tweede term is 3·2√(5x+3) en deze termen worden van elkaar afgetrokken (je mag ook zeggen: de tweede term is -3·2√(5x+3) en deze wordt bij de eerste opgeteld). Wanneer je 3·2√(5x+3) in zijn geheel vermenigvuldigt met √(5x+3), dan is deze gehele term √(5x+3) keer zo groot geworden. Je moet dus niet de factor 3 en de factor 2 beide vermenigvuldigen.

Je kunt dit inzien wanneer je beseft dat je deze term ook eerst kunt vereenvoudigen (3·2=6):

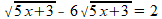
Ik denk niet dat je de tweede term nu nog twee keer met de wortel zou willen vermenigvuldigen!

Je kunt zelfs nog verder vereenvoudigen:

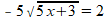
Dus:

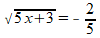
Nu zien we dat deze vergelijking geen oplossing heeft, omdat een wortel niet gelijk kan zijn aan een negatief getal.

Vragen naar aanleiding van dit antwoord? Klik rechts..!
dinsdag 20 juni 2017