|
|
|
\require{AMSmath}



Kansrekenen
Hallo,
Bij oefeningen kansrekening gaat men soms gebruik maken van de formule van laplace (teller en noemer) maar soms wordt er ook wel gebruik gemaakt van bv om een opgave op te lossen V (3 bovenaan en 5 onderaan bv) maar zonder noemer. Hoe kan je nu precies weten wanneer je een opgave krijgt dat je het met de formule van laplace moet doen of op manier 2?
Mvg, Elise
Elise
Leerling bovenbouw havo-vwo - maandag 5 juni 2017
Antwoord
Hallo Elise,
Ik begrijp niet goed wat je bedoelt met bv '3 bovenaan en 5 onderaan, maar zonder noemer'. Wellicht bedoel je de notatie voor aantal combinaties, zoals:
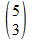
Dit wordt vaak uitgesproken als '5 boven 3'. Er staat géén breukstreep tussen deze getallen, want dit betekent iets heel anders dan een breuk! Ik kom hierop terug, maar eerst even de formule van Laplace, ook wel de kansdefinitie van Laplace genoemd.
Deze kansdefinitie van Laplace kan je gebruiken om een kans te berekenen wanneer alle mogelijke uitkomsten even waarschijnlijk zijn. Bijvoorbeeld:
- Je trekt uit een kaartspel een willekeurige kaart. Wat is de kans dat dit een hartenkaart is?
Volgens de formule van Laplace moet je nu drie dingen doen:
- Tel het aantal mogelijke gunstige uitkomsten (dus: wat voldoet aan de vraag).
In dit geval: er zijn 13 hartenkaarten, dus 13 mogelijke gunstige uitkomsten
- Tel het totaal aantal mogelijke uitkomsten.
In dit geval: er zijn 52 kaarten die je kunt trekken, dus 52 mogelijke uitkomsten.
- Deel het eerste aantal door het tweede aantal.
In dit geval: de kans op een hartenkaart is 13/52=1/4
Je ziet: een breuk.
In dit geval is het niet zo lastig om het aantal mogelijke gunstige uitkomsten en het totaal aantal mogelijke uitkomsten te tellen. Maar bij andere vragen kan dit tellen wel moeilijk zijn. Vandaar dat je op school ook 'telproblemen' leert oplossen. Bij deze vraag wordt het tellen een stuk lastiger:
- Je trekt 3 kaarten. Hoe groot is de kans dat dit 3 hartenkaarten zijn?
Nu moeten we dus tellen hoeveel mogelijkheden er zijn om 3 hartenkaarten uit een kaartspel te trekken. Waarschijnlijk heb je geleerd dat je hier te maken hebt met combinaties: je moet 3 'dingen' (=hartenkaarten) kiezen uit 13 hartenkaarten, zonder terugleggen. Het aantal mogelijkheden hiervoor is het aantal combinaties van 3 uit 13, dit noteren we als:
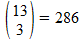
Let op: géén breukstreep, want dit is geen breuk! Het is ook geen kans, het is slechts het tellen van een aantal mogelijkheden: er zijn 286 mogelijkheden om 5 hartenkaarten uit 13 hartenkaarten te trekken.
Nu we het aantal mogelijke gunstige uitkomsten hebben, moeten we ook het totaal aantal mogelijke uitkomsten vinden. We kiezen 3 'dingen' (=willekeurige kaarten) uit een totaal van 52. Ook nu is dit een aantal combinaties, 3 uit 52:
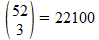
Ook nu: géén breukstreep, het is geen kans, maar een aantal mogelijkheden: er zijn 22100 mogelijkheden om 3 willekeurige kaarten uit 52 te trekken.
Nu zijn we klaar met tellen, en kunnen we met de kansdefinitie van Laplace de gevraagde kans berekenen:
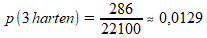
Samengevat:
- Met behulp van de kansdefinitie van Laplace kunnen we een kans op een gebeurtenis berekenen wanneer we een aantal gunstige mogelijkheden weten en een totaal aantal mogelijkheden (alle mogelijkheden moeten wel even waarschijnlijk zijn), de berekening is een deling (breuk);
- Met behulp van het formuletje voor een aantal combinaties kunnen we mogelijkheden tellen, we noteren dit als twee getallen boven elkaar (géén breuk) tussen haken.
Is dit wat je bedoelt?

|
Vragen naar aanleiding van dit antwoord? Klik rechts..!
maandag 5 juni 2017
|

|



home |
vandaag |
bijzonder |
gastenboek |
statistieken |
wie is wie? |
verhalen |
colofon
©2001-2024 WisFaq - versie 3
|








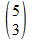
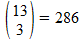
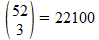
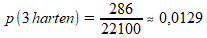


 Re: Kansrekenen
Re: Kansrekenen