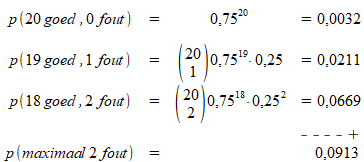WisFaq!

De digitale vraagbaak voor het wiskundeonderwijs

HOME

samengevat

\require{AMSmath}

Partij artikelen

Uit grote partijen artikelen neemt men steekproeven van 20 stuks. Een partij wordt afgekeurd als in zo'n steekproef 3 of meer foutieve exemplaren worden aangetroffen. a) wat is de kans dat een partij met 25% fouten wordt afgekeurd? b) wat is de kans dat van 10 partijen met elk 10% fouten er 8 of meer goedgekeurd worden?

Antwoord: a) 0.909 b)0.324

Berekening?
Roan
Student universiteit - dinsdag 23 mei 2017

Antwoord

Hallo Roan,

Uit een partij wordt 20 keer een artikel genomen, steeds met een kans op afkeur van 0,25 en een kans op goedkeuring van 0,75. Het aantal goedgekeurde (of afgekeurde) artikelen is dan binomiaal verdeeld.

In dit geval is het handig om de kans te berekenen dat een partij wordt goedgekeurd. Dit is het geval wanneer het aantal foutieve exemplaren 0, 1 of 2 is. De kansen hierop zijn:

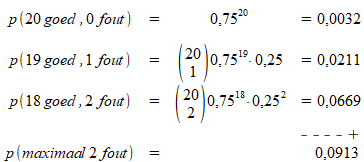
De kans dat een partij wordt goedgekeurd, is 0,091. De kans dat een partij wordt afgekeurd, is dan 1-0,091 = 0,909.

Veel rekenmachines en computerprogrammaatjes kunnen deze berekening in één keer uitvoeren. Dit hulpje berekent de kans dat je in een steekproef van 20 stuks maximaal 17 goede exemplaren vindt, dus de partij zult afkeuren:Voor vraag b) ga je als volgt te werk:
Bereken eerst op dezelfde wijze de kans dat je een partij goedkeurt (dus maximaal 2 foutieve exemplaren aantreft). Je vindt p(max 2 fout)=0,6769, dus p(afkeur)=0,3231
Wanneer je dit kansexperiment 10 keer uitvoert, is het aantal afgekeurde partijen ook weer binomiaal verdeeld met p(afkeur)=0,3231.
Op dezelfde wijze bereken je dan de kans dat je, bij 10 keer uitvoeren van dit experiment, 2 of minder partijen afkeurt:
Lukt het hiermee?

Vragen naar aanleiding van dit antwoord? Klik rechts..!
dinsdag 23 mei 2017