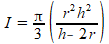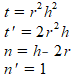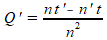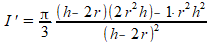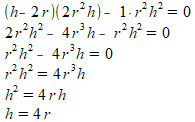|
|
|
\require{AMSmath}



Re: Re: Re: Re: Re: Bol in een kegel
Hoi Gilbert,
Ik krijg dan uit h = 0 of h = -2. Ik vermoed dat ik dan de fout inga bij de afgeleide. Klopt het dat als je de gegevens invult in de formule van de inhoud dat je de volgende formule uitkrijgt na herleiden? 1/3pi ∑ h2 ∑ r2 (:) (h-2r). Hierdoor krijg ik een afgeleide, maar kom dan alsnog op het foute antwoord uit.
Didier
Leerling bovenbouw havo-vwo - zaterdag 13 mei 2017
Antwoord
Hallo Didier,
De formule voor de inhoud van je kegel is correct:
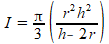
Kennelijk gaat er iets mis met differentiŽren of herleiden.
Tussen haakjes staat een quotiŽnt. De teller noem ik even t, de noemer is n. Ik bereken ook alvast de afgeleide t' van de teller en de afgeleide n' van de noemer naar h, dus:
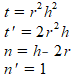
De afgeleide Q' van zo'n quotiŽnt bereken je met de quotiŽntregel:
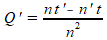
De afgeleide I' van de inhoud wordt hiermee:
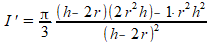
We zoeken de waarde van h waarvoor I'=0. Voldoende is om de teller van de breuk gelijk aan nul te stellen. Het herleiden gaat dan als volt:
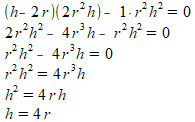
Kan je zelf vinden waar jouw berekening mis ging?

|
Vragen naar aanleiding van dit antwoord? Klik rechts..!
zaterdag 13 mei 2017
|

|



home |
vandaag |
bijzonder |
gastenboek |
statistieken |
wie is wie? |
verhalen |
colofon
©2001-2024 WisFaq - versie 3
|








 Dit is een reactie op vraag 84411
Dit is een reactie op vraag 84411