WisFaq!

De digitale vraagbaak voor het wiskundeonderwijs

HOME

samengevat

\require{AMSmath}

Re: Re: Re: Re: Smartie in vierkant

Dit is een reactie op vraag 84335

Als ik het goed heb gedaan is de uitwerking:

p=√(a²+b²)

We blijven wat moeite hebben met het begrijpen van deze logica:

'De halve assen a en b zijn evenredig met de zijde van het vierkant, dus voor andere afmetingen van het vierkant kan je eenvoudig opschalen. Bij een zekere verhouding van van a en b is L evenredig met a.

Peter,
Student hbo - donderdag 27 april 2017

Antwoord

Hallo Peter, Onno, Awad en Sam,

Je uitwerking is correct. Bedenk dat we voor de zijde L van het vierkant hebben gekozen:

L=p·√2

dus:

p=L/√2

Invullen in jullie uitwerking levert:

√(a²+b²)=L/√2

Dit is hetzelfde verband als ik eerder aangaf. Immers, links en rechts van het is-gelijk-teken kwadrateren levert:

a²+b²=L²/2

Conclusie: een elliptische vorm met halve assen a en b past (schuin) binnen een vierkant met zijde L wanneer geldt:

a²+b²$\le$¹/₂L²

Dit was jullie vraag, toch?

Wat betreft de logica achter de genoemde evenredigheid: we hadden al gevonden dat een ellips met halve assen a en b precies in een vierkant met zijden √2 past wanneer geldt:

a²+b²=1

Zo'n ellips is links in onderstaande figuur getekend:

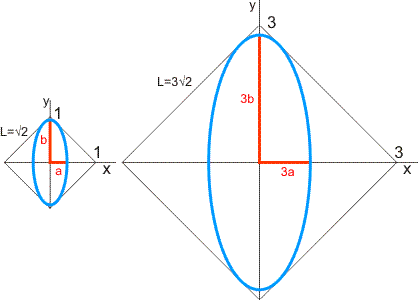
Wanneer we a en b 3 keer zo groot kiezen, dan moet de zijde van het vierkant ook 3 keer zo groot worden om de nieuwe ellips precies te laten passen, zie de rechter figuur. Het hele plaatje is 'gewoon' 3 keer zo groot. Andersom geredeneerd: maak je de zijde van het vierkant 5 keer zo groot, dan mogen a en b ook 5 keer zo groot worden, dan past deze ellips ook weer precies binnen het vierkant. Meer dan dit is het niet ...

OK zo?

Vragen naar aanleiding van dit antwoord? Klik rechts..!
donderdag 27 april 2017