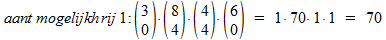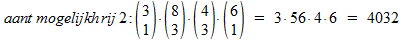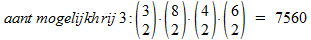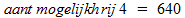WisFaq!

De digitale vraagbaak voor het wiskundeonderwijs

HOME

samengevat

\require{AMSmath}

Re: Telprobleem

Dit is een reactie op vraag 71944

Beste

Ik zit echt vast met het uitrekenen van de som. Hoe kan je die berekenen? Ik heb al combinaties geprobeerd, maar niets lukt. Kunt u me helpen?

Alvast bedankt!
Emily
3de graad ASO - woensdag 22 maart 2017

Antwoord

Hallo Emily,

Ik vat de vraag nog een keer samen:
Groep 1 bestaat uit 3 mannen en 8 vrouwen (=11 personen)
Groep 2 bestaat uit 4 mannen en 6 vrouwen (=10 personen)
Kies uit beide groepen 4 personen, zodanig dat je in totaal 4 mannen en 4 vrouwen kiest.
Eerst bekijken we welke samenstellingen allemaal mogelijk zijn:
Je kunt uit de eerste groep 0 mannen kiezen. Dan moet je uit deze groep 4 vrouwen kiezen (want totaal 4). Uit de tweede groep moet je dan 4 mannen en 0 vrouwen kiezen om in totaal 4 mannen en 4 vrouwen te krijgen.
Je kunt uit de eerste groep ook 1 man kiezen. Dan moet je uit deze groep 3 vrouwen kiezen (=4 totaal). Uit de tweede groep moet je dan 3 mannen kiezen en 1 vrouw (want totaal 4 mannen en 4 vrouwen).

Zo kunnen we doorgaan. In de onderstaande tabel zie je alle mogelijkheden. Tussen haakjes staat steeds hoeveel personen in een groep zitten:

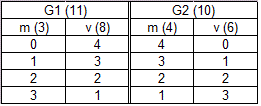
Eén mogelijke samenstelling ontbreekt: 4 mannen uit de eerste groep. Maar dit is geen mogelijkheid, want in deze groep zitten maar 3 mannen.

Nu gaan we van elke rij berekenen op hoeveel manieren dit kan.

In de eerste rij zie je dat je moet kiezen:
0 mannen uit 3, èn 4 vrouwen uit 8, èn 4 mannen uit 4, èn 0 vrouwen uit 6. Het aantal mogelijkheden voor deze keuzes zijn steeds combinaties, we krijgen:

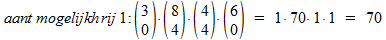
Voor rij 2 moeten we kiezen:
1 man uit 3, èn 3 vrouwen uit 8, èn 3 mannen uit 4, èn 1 vrouw uit 6. Het aantal mogelijkheden is:

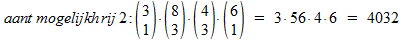
Zo vinden we voor rij 3:

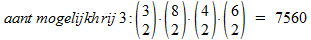
En voor rij 4:

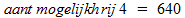
Wanneer je deze aantallen mogelijkheden optelt, krijg je het totaal aantal mogelijkheden om een groep samen te stellen: 12302.

Is het probleem hiermee opgelost?

Vragen naar aanleiding van dit antwoord? Klik rechts..!
zaterdag 25 maart 2017