|
|
|
\require{AMSmath}



Stelling van Thales over evenwijdige lijnen
Voor het vak wiskunde moet ik een aantal basiseigenschappen vanaf het tweede jaar S.O. kunnen bewijzen. Eťn ervan luidt als volgt:
Als drie evenwijdige rechten gesneden worden door twee andere rechten, dan is de verhouding van de lijnstukken afgesneden door de ene snijlijn gelijk aan de verhouding van de lijnstukken afgesneden door de andere snijlijn.
Ik heb nu al overal gezocht op internet en ik kwam tot het besluit dat dit de stelling van Thales is, is dit zo? (Want als ik dan naar de stelling van Thales zoek op internet vind ik altijd dat de stelling van Thales luidt als volgt: het midden van de schuine zijde van een rechthoekige driehoek is het middelpunt van de omgeschreven cirkel.) Kan u mij helpen met dit bewijs?
Ook moet ik het omgekeerde van deze eigenschap bewijzen:
Als drie rechten gesneden worden door twee andere rechten en als de verhouding van de lijnstukken op de ene snijlijn gelijk is aan de verhouding van de lijnstukken op de andere snijlijn, dan zijn de drie rechten evenwijdig.
Kan u me hierbij ook helpen?
Hartelijk dank!
elke
Student Hoger Onderwijs BelgiŽ - dinsdag 8 februari 2005
Antwoord
Dag Elke,
Inderdaad ook deze stelling wordt wel aan Thales toegeschreven.
Maar nergens in de geschiedschrijving over de wiskunde (althans in betrouwbare klassieke bronnen) is er een vindplaats waar dit wordt bevestigd.
Het zijn er in ieder geval 5 of 6, maar de door jou genoemde stelling staat daar niet bij.
Ook in de Elementen van Euclides komt de stelling (voor zover ik mij herinner) in deze vorm niet voor.
Gegeven (Stelling van Thales?):
De evenwijdige lijnen l1, l2, l3 die van de lijn m de lijnstukken a1, a2 en van de lijn n de lijnstukken b1, b2 afsnijden.
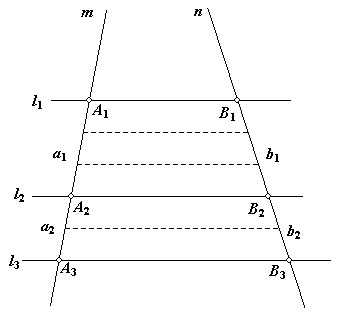 [figuur 1] [figuur 1]
Te bewijzen (zie figuur 1):
a1 / a2 = b1 / b2
Bewijs:
Stel a1 / a2 = p / q met p en q gehele getallen (in de tekening is p = 3 en q = 2).
We denken a1 dan verdeeld in p gelijke delen en a2 in q gelijke delen.
Door de deelpunten (op m) trekken we lijnen evenwijdig aan l1.
Nu is A1A3 in p + q gelijke delen verdeeld.
Is dat dan ook het geval voor B1B3?
Het antwoord is JA, maar dat moeten we echt OOK bewijzen (bewijs volgt...)
Dan liggen p van die gelijke delen op B1B2 en q van die gelijke delen op B2B3.
Zodat:
b1 / b2 = p / q
en dus a1 / a2 = b1 / b2.
Nu eerst maar de eigenschap die we hierboven (hoeveel keer?) gebruikten. Hulpstelling.Als enige evenwijdige lijnen van een lijn gelijke stukken afsnijden, dan snijden zij van elke andere lijn gelijke stukken af.
Gegeven:
De evenwijdige lijnen l1, l2, l3 snijden van de lijn m de gelijke stukken A1A2, A2A3 af en van de lijn n de stukken B1B2, B2B3.
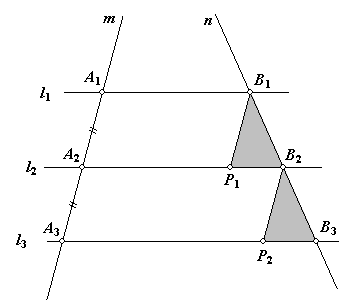 [figuur 2] [figuur 2]
Te bewijzen (zie figuur 2):
B1B2 = B2B3
Bewijs:
Trek B1P1, B2P2 beide // m.
Dan ontstaan de parallellogrammmen A1A2P1B1 en A2A3P2B2.
Direct duidelijk is dan dat A1A2 = B1P1 = A2A3 = B2P2
en dan zijn de driehoeken B1P1B2 en B2P2B3 congruent (waarom is dat zo?).
Waaruit volgt dat B1B2 = B2B3.
Tja, de eerste stelling (die van Thales dus), hebben we hierboven alleen bewezen voor gehele getallen.
Als p en q rationale getallen zijn, dan is de verhouding p / q terug te brengen tot een verhouding van gehele getallen.
Bijvoorbeeld:
(31/3) / (21/2) = 4 : 3
Zijn p en q reŽle getallen, dan wordt het bewijs echter een stuk ingewikkelder.
Veelal wordt dan opgemerkt, dat met behulp van rijen rationale getallen (die die reŽle getallen benaderen) het bewijs ook geleverd kan worden.
En dat doe ik nu dus ook maar.
En dan de omgekeerde stelling. We formuleren deze liever als:
Als drie lijnen, waarvan er twee evenwijdig zijn van twee snijlijnen evenredige stukken afsnijden, dan is ook de derde lijn evenwijdig met de eerste twee.
Dus...
Gegeven:
l1 // l2
l1, l2, l3 snijden van m en n stukken a1, a2 en b1, b2 af met a1 / a2 = b1 / b2.
Te bewijzen:
l1, l2, l3 zijn evenwijdig
Bewijs (maak zelf een tekening):
Uit het ongerijmde...
Stel l3 is niet evenwijdig met l1 en l2.
We trekken nu door A3 de lijn x evenwijdig met l2 (dat kan; waarom?).
x snijdt de lijn n in het punt Y.
De punten B3 en Y vallen dan niet samen (waarom?).
Stellen we nu B2Y = c, dan geldt:
- a1 / a2 = b1 / b2 (volgens het gegeven)
- a1 / a2 = b1 / c (volgens de stelling van Thales, hierboven)
zodat
b1 / b2 = b1 / c
waaruit volgt dat b2 = c
Met andere woorden B3 valt (toch) samen met Y. En dit leidt tot een tegenspraak, waaruit dan weer volgt dat l3 // l2 // l1.
Je schrijft dat je overal op internet gezocht hebt. Dat je niets gevonden hebt, kan wel kloppen.
Immers, niet alles staat op internet. Daar onvindbare, maar wel bestaande zaken staan, bijna zeker, in boeken (en die staan op hun beurt wel weer in bibliotheken).
Maar nu staat het in ieder geval ook op internet!
|
Vragen naar aanleiding van dit antwoord? Klik rechts..!
woensdag 9 februari 2005
|

|



home |
vandaag |
bijzonder |
gastenboek |
statistieken |
wie is wie? |
verhalen |
colofon
©2001-2024 WisFaq - versie 3
|








 [figuur 1]
[figuur 1] [figuur 2]
[figuur 2]
