WisFaq!

De digitale vraagbaak voor het wiskundeonderwijs

HOME

samengevat

\require{AMSmath}

Ingeschreven cirkel in apart soort driehoek

Situatie:
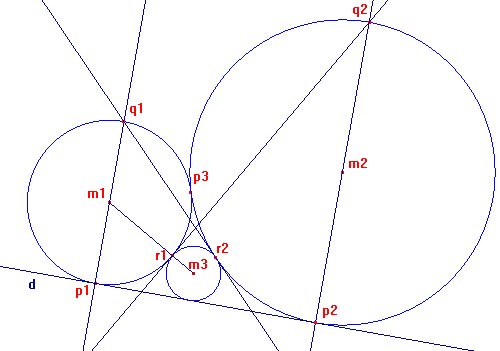
Er zijn twee cirkels: [c1] en [c2]. Deze cirkels hoeven niet even groot te zijn. Er is ook één lijn: [d]. Deze lijn raakt de twee cirkels (maar gaat niet door het punt waar de twee cirkels elkaar raken). De punten waar de cirkels [c1] en [c2] de lijn [d] raakt, heten [p1] en [p2]. Het punt waar de cirkels elkaar raken, heet [p3].
Zo ontstaat er een soort driehoek, waar van de twee zijden bogen zijn ([p1][p3] en [p2][p3]) en de derde zijde een lijnstuk ([p2][p3]).

Gevraagd is het middelpunt van de ingeschreven cirkel van de aparte driehoek [p1][p2][p3].

(Dit is geen huiswerk; dit heb ik zelf allemaal bedacht. Ik wilde namelijk een variatie op de zeef van Sierpinski maken en ik stuitte op onder andere dit probleem.)

Per toeval heb ik het antwoord met behulp van Cabri ontdekt:
Als je de loodlijnen [l1] en [l2] tekent op de lijn [d] door resp. punt [p1] en [p2], snijden deze lijnen de cirkels óók bij de punten [q1] resp. [q2]. Als je door [q1] een raaklijn tekent aan [c2] en door [q2] een raaklijn aan [c1] (allebij aan de kant van waar het gevraagde middelpunt ligt), zijn deze raaklijnen samen met de lijn [p1][p2] de driehoek met dezelfde ingeschreven cirkel als van de aparte driehoek [p1][p2][p3].

Wat is nu het probleem?

Ik heb geen flauw idee hoe ik dit moet bewijzen. En hoewel ik heb geprobeerd een bewijs te vormen via hyperbooltakken (de conflictlijnen tussen de cirkels onderling en de cirkels met de lijn)(maar daarvan weet ik te weinig af) en via de omgeschreven cirkel van de driehoek met als hoekpunten de raakpunten van de door [q1] en [q2] getekende raaklijnen en een punt op [d], kom ik er nog steeds niet uit.

Weet iemand een oplossing?
Stijn
Leerling bovenbouw havo-vwo - donderdag 3 juni 2004

Antwoord

dag Stijn,

Mooi probleem!
Het heeft me heel wat hoofdbrekens gekost, maar het is gelukt! Achteraf niet moeilijk, maar dat is gemakkelijk zeggen achteraf !
Het toverwoord is hier: de macht van een punt t.o.v. een cirkel.
Als we kunnen bewijzen dat de macht van q1 t.o.v. c2 gelijk is aan de macht van q1 t.o.v. c3, (en iets dergelijks voor q2), dan zijn we klaar: dan ligt q1 namelijk op de machtlijn van c2 en c3, dus op de gemeenschappelijke raaklijn.
Noem R1, R2 en R3 de stralen van de drie cirkels.
Noem r3 het raakpunt van c3 met lijn d.
Je kunt dan p1r3² uitrekenen:
p1r3² = (R1+R3)² - (R1-R3)² = 4·R1·R3
Evenzo:
p1p2² = (R2+R1)² - (R2-R1)² = 4·R1·R2
De macht van q1 t.o.v. c3 is gelijk aan q1m3² - R3²
Nu kun je q1m3² ook weer (met Pythagoras) uitrekenen, gebruik makend van bovenstaande p1r3².
De rest van het bewijs laat ik aan jou over.
Kom je er niet uit, dan hoor ik het nog.
Zoek ook eens op internet naar Sangaku, waar een schat aan informatie te vinden is over rakende cirkels, bijvoorbeeld onderstaand artikel uit het tijdschrift Pythagoras.
Veel plezier!
groet,
Zie Sangaku

Vragen naar aanleiding van dit antwoord? Klik rechts..!
maandag 7 juni 2004