WisFaq!

De digitale vraagbaak voor het wiskundeonderwijs

HOME

samengevat

\require{AMSmath}

Re: Differentieerbaarheid onderzoeken

Dit is een reactie op vraag 11270

Beste wisfaq,
Bedankt voor het beantwoorden van mijn vragen,maar doordat mijn opgaven onleesbaar is geworden en u antwoordt niet echt duidelijk is voor mij omdat alles zo erg "druk" uitziet op het scherm begrijp ik het niet meer zou u anders het volgende sommetje als voorbeeld kunnen nemen ?
Wilt u a.u.b korte stapjes nemen zodat ik het kan bestuderen hoe u aan uw antwoordt komt.

Dit is het sommetje:

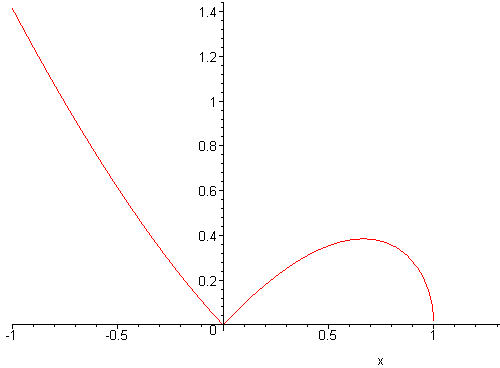
1) f(x)=Öx²-x³ met domein - ,1 ]

a) Onderzoek of f differntieebaar is in O.
b) Onderzoek of f links-differentieerbaar is in 1.

Alvast bedankt
Met vriendelijke groet,
Tim
tim
Leerling bovenbouw havo-vwo - maandag 19 mei 2003

Antwoord

f(x)
= Ö(x²-x³)
= Ö(x²)Ö(1-x)
= |x|Ö(1-x)

waarin |x| de absolute waarde voorstelt van x (|x|=x voor positieve x, |x|=-x voor negatieve x)

Afleidbaarheid in x=0

f'(0)
= lim{x®0}[f(x)-f(0)]/[x-0]
= lim{x®0}[|x|Ö(1-x)]/x

Hier komt nu de zebra uit de onderbroek. De limiet voor x®0 betekent eigenlijk dat we x OP WELKE MANIER DAN OOK naar 0 laten naderen. Maar de limiet waar we hier mee te maken hebben, hangt WEL af van de manier waarop we het punt x=0 naderen:

Naderen we x=0 bijvoorbeeld langs de positieve kant, dan is |x|/x = +1 en is de limiet gelijk aan +1.

Naderen we x=0 langs de negatieve kant, dan is |x|/x = -1 en is de limiet gelijk aan -1.

De linkerlimiet bestaat dus wel, en de rechterlimiet bestaat ook wel, maar ze hebben een verschillende waarde, en dus we kunnen niet zomaar het woord "limiet" gebruiken.

De functie f(x) is dus niet differentieerbaar in x=0, omdat de linkerafgeleide en de rechterafgeleide er verschillende waarden aannemen.

(Merk op dat er nog andere manieren zijn om x naar nul te laten gaan, bijvoorbeeld door altijd maar dichter heen en weer te springen rond 0. Maar voor het niet-bestaan van de limiet volstaat het om aan te tonen dat er zeker 2 manieren zijn die verschillende resultaten opleveren.)

Linkerafleidbaarheid in x=1

Ik gebruik symbolen als lim{x®a-} en lim{x®a+} om aan te duiden dat x nadert tot a via waarden die kleiner dan wel groter zijn dan a.

f'(1)
= lim{x®1-}[f(x)-f(1)]/[x-1]
= lim{x®1-}[|x|Ö(1-x)]/[x-1]
= lim{x®1-}[-|x|]/Ö(1-x)
= -¥

De functie is dus niet linksafleidbaar in x=1 omdat de afgeleide in die buurt onbegrensd wordt.

Vragen naar aanleiding van dit antwoord? Klik rechts..!
maandag 19 mei 2003

Re: Re: Differentieerbaarheid onderzoeken