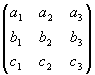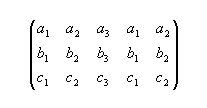WisFaq!

De digitale vraagbaak voor het wiskundeonderwijs

HOME

samengevat

\require{AMSmath}

Hoe bereken je de determinant van een matrix?

Gegeven het stelsel lineaire vergelijkingen Ax = b. Dat is een vraag en matrix van mijn oefententamen van mijn ter voorbereiding van me her van morgen. Alleen ik weet niet wat een determinant is en hoe ik deze kan berekenen. Tijdens het vak zijn alleen de rekenmethodes van Gauss en Gauss-Jordan behandeld.
Bij voorbaat dank.
Mark
Student hbo - donderdag 26 juni 2003

Antwoord

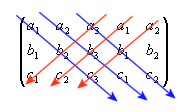
Een algemene manier om de determinant van een matrix te berekenen, vind je op http://mathworld.wolfram.com/Determinant.html, maar een vlotte manier om van een 3x3 matrix de determinant te berekenen, is de volgende:

Ga uit van de 3x3 matrix

breidt deze aan de rechterkant uit met de 1e twee kolommen:

Tot slot teken (of denk) je 6 pijltjes zoals aangegeven.

Langs elke pijl neem je het produkt van de 3 getallen die langs deze pijl staan. De produkten langs de blauwe pijlen tel je op, die langs de rode pijlen trek je er weer vanaf. Dus:

determinant= a₁b₂c₃ + a₂b₃c₁ + a₃b₁c₂ - a₃b₂c₁ - a₁b₃c₂ - a₂b₁c₃

Bij een 2x2 matrix is 't nog wat eenvoudiger:
determinant = a₁b₂ - a₂b₁

groeten,
martijn

Vragen naar aanleiding van dit antwoord? Klik rechts..!
vrijdag 27 juni 2003