
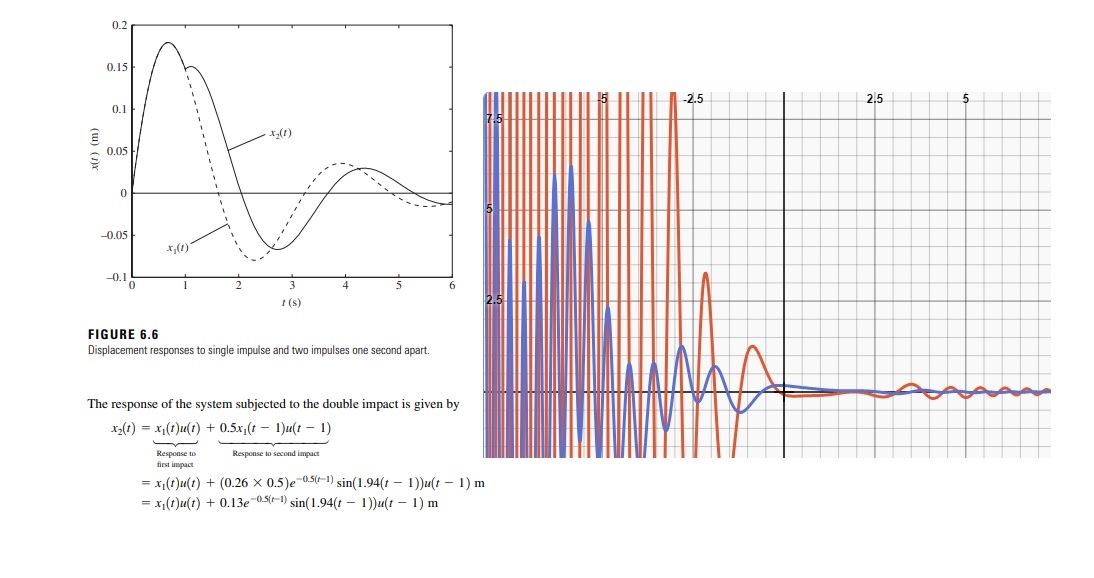
Respons impact
beste ik heb de volgende functie ingevoerd op https://www.derivative-calculator.net/:
f(x)=0,26e^(-0,5x)*(sin1,94x)*0,5+[0,13e^(-0,5(x-1))*sin(1,94(x-1)0,5(x-1)]
Ik krijg echter niet de dubbele respons als vermeld in de bijlage, ik vermoed dat ik de puls niet goed heb ingevoerd, de functie van de dubbele impact is
f(t) = $\delta $ (t)+0,5 $\delta $ (t-1)
de functie van de uitwijking is x(t)=0,26e^(-0,5x)*(sin1,94x)
gijs
Student hbo - donderdag 31 augustus 2023
Antwoord
Je bent erg slordig geweest.
In het linker plaatje komt nog een functie $u(t)$ voor, die zie ik in je invoer niet meer terug. Die is wel belangrijk; het is de Heavisidefunctie:
$$u(t)=\begin{cases} 0 & \text{als }t < 0\\ 1 &\text{als }t\ge0\end{cases}
$$De $0{,}5$ bij de eerste term zie ik dan weer niet in het plaatje. Kortom: de eerste term in $f(x)$ zou moeten zijn
$$0{,}26e^{-0{,}5x}\cdot\sin(1{,}94x)\cdot u(x)
$$en als je in het plaatje kijkt deugt je tweede term ook niet: je hebt $0{,}13$ genomen (de helft van $0{,}26$) maar je vermenigvuldigt later nog een keer met $0{,}5$; in $\sin(1{,}94(x-1))$ ontbreekt het laatste haakje; en je vermenigvuldigt met $x-1$ in plaats van $u(x-1)$.
De tweede term moet dus
$$0{,}13e^{-0{,}5(x-1)}\cdot\sin(1{,}94(x-1))\cdot u(x-1)
$$zijn.
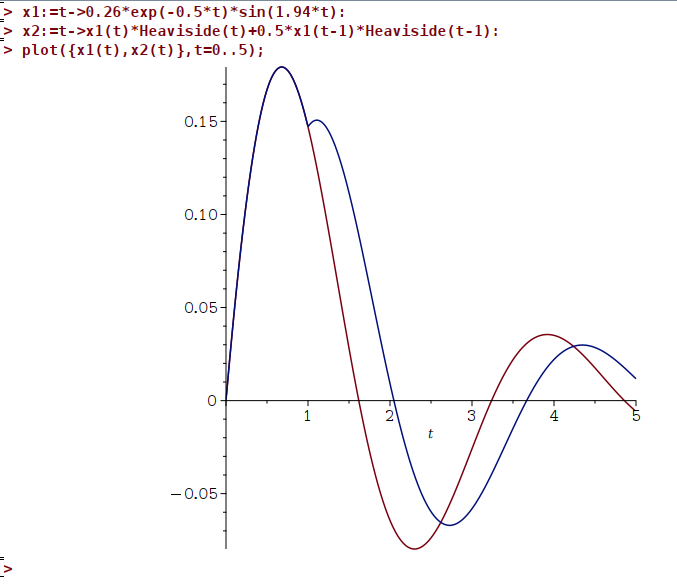
In Maple gaat het zo:
kphart
donderdag 31 augustus 2023
 ©2001-2024 WisFaq
©2001-2024 WisFaq
|