Re: Bewijs voor de afgeleide van een exponentiele functie

Dit is een reactie op vraag 34216

Maar wat is dan het bewijs dat a^x = e^u(x) waarbij u(x)=x(ln(a)).

Waar ik eigenlijk benieuwd naar was is de uitwerking van de formule a^x invullen in de formule (f(x+h)-(f(x)))/h
waarbij h=1/oneindig. Dus:

(a^x+h-a^x)/h

daar komt op een gegeven moment, als het goed is, uit:
a^x maal een breuk die een constante blijkt te zijn, namelijk ln(a).
Zodat het bewezen is. Maar zelf kwam ik er niet uit.

Liewe
Leerling bovenbouw havo-vwo - woensdag 23 februari 2005

Antwoord

Je eerste vraag.
Volgens een eigenschap van de logaritmen is: ln(a^x) = x·ln(a)
waaruit dan onmiddellijk volgt dat: e^x·ln(a) = a^x
OF
schrijf a als macht van e.
Los daartoe p op uit: a = e^p. Dit geeft: p =ln(a).
Dan is:
a^x = (e^p)^x = e^x·p

Met je tweede vraag zitten we dicht bij de grondbeginselen van de exponentiële functies.
Belangrijk daarbij is ondermeer hoe de functie e^x gedefinieerd is; en, daarmee samenhangend, de functie ln(x).
Om het eenvoudig te houden denk ik toch maar bovenstaande 'omschrijfwijze' voor a^x te gebruiken.

Vooraf: ik gebruik de volgende eigenschap:
......(*)
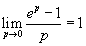Kijk zelf eens hoe je die eigenschap kan bewijzen!!
Aanwijzing: bedenk dat e⁰ = 1 en gebruik ook de limietdefinitie voor de afgeleide van e^x voor x = 0.

Zij f(x) = a^x, dan is:
f(x + h) - f(x) = a^x+h - a^x = a^x(a^h - 1)
We moeten nu, na deling van bovenstaande uitdrukking door h, onderzoeken (jouw hierboven bedoelde breuk):

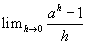
Omgeschreven geeft dit:

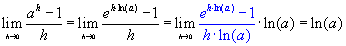
Hierin is de eigenschap (*) gebruikt; ga zelf na hoe!

Bewijs geleverd!

woensdag 23 februari 2005

©2001-2024 WisFaq