|
|
|
\require{AMSmath}



Snijpunt tussen een lijn en een vlak
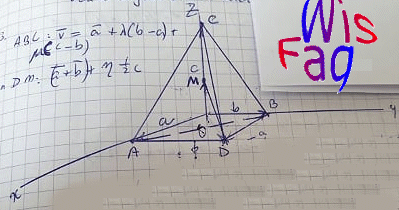
Op een orthnormale basis is gegeven de piramide C.OADB waarvan het grondvlak een rechthoek is. a, b en c zijn plaatsvectoren van A, B en C. M is het midden van OC.- Bepaal een vectorvoorstelling van vlak ABC.
Hierbij had ik v=a+l(b-a)+m(c-b) wat zij ook hebben.- Bepaal de plaatsvector s van het snijpunt S van de lijn DM met vlak ABC.
Nu is het zo dat voor de lijn DM een andere vector voorstelling heb dan zij en derhalve ook een ander snijpunt. Ik heb geprobeerd mijn vectorvoorstelling te herzien en hun vector voorstelling te begrijpen maar dat lukt me helaas niet.
Ik had als vector voorstelling van lijn DM: (a+b)+e(c/2). Zij hebben (a+b)+e(a+b-c/2). Dat kan ik niet uit de tekening van mij op maken die ik heb opgestuurd kan iemand mij mischien hier op weg helpen?
mboudd
Leerling mbo - donderdag 23 januari 2020
Antwoord
Je hebt als vector voorstelling van lijn DM: (a+b)+e(c/2) genomen maar dat klopt niet. Met a+b zit je in D, jij gaat nu met c/2 recht omhoog maar dat klopt niet. Je moet eerst naar O (dat is -a-b) en dan c/2 omhoog.
Dus lijn(DM) = a + b + $\lambda$(-a-b+c/2)
In plaats van -a-b+c/s kan je echter ook a+b-c/2 nemen. Dat is dezelfde vector maar dan in tegengestelde richting, maar dat is niet erg want dat geeft dezelfde lijn.
Helpt dat?

|
Vragen naar aanleiding van dit antwoord? Klik rechts..!
donderdag 23 januari 2020
|

|



home |
vandaag |
bijzonder |
gastenboek |
statistieken |
wie is wie? |
verhalen |
colofon
©2001-2024 WisFaq - versie 3
|











 Re: Snijpunt tussen een lijn en een vlak
Re: Snijpunt tussen een lijn en een vlak