|
|
|
\require{AMSmath}
Vierkant en driehoeken
Hallo Wisfaq,
Het lukt me niet een plaatje te maken maar ik probeer het zo.
Een vierkant ABCD met zijde x wordt aan de bovenzijde in 2 gelijke delen(x/2) gedeeld.Van daaruit teken ik een rechthoekige driehoek met rechte hoek op het punt waar de halve zijde bovenaan zich bevindt .Hoek F =90° Trek nu FB uit dit punt F naar het punt B op het vierkant onderaan rechts en FE naar de zijde van het vierkant op de linkerzijde . Bereken nu de hoek gelegen onder hoek E en aansluitend op de linkerzijde van het vierkant.
Oef....
Groetjes en dank voor je antwoord alvast nu !!
Rik
Rik Le
Iets anders - woensdag 20 oktober 2010
Antwoord
Hoi Rik,
Ik verwacht, dat je onderstaande tekening zo'n beetje bedoeld:
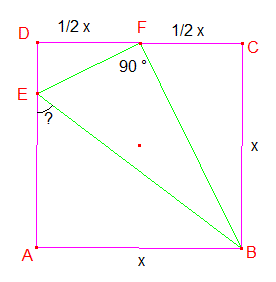
ÐBFE=90 graden
Dus: ÐEFD + ÐBFC = 90 graden
(gebruik gemaakt van: gestrekte hoek van 180 graden)
In DBCF geldt:
ÐFBC + ÐBFC = 90 graden
Dus: ÐEFD = ÐFBC
Conclusie: DEFD~DFBC (gelijkvormig)
BC/FD=FC/ED
x/1/2x=1/2x/ED
ED=1/4x
Dan AE=3/4x
Kijk nu in DABE:
tan(ÐAEB)=x/3/4x=4/3
ÐABE=tan-1(4/3) 53°
Hopelijk volg je mijn denkstappen. Denk er waal aan dat dit één manier is, er zijn nog andere volgroutes om de som op te lossen.
Mvg Thijs Bouten
|
Vragen naar aanleiding van dit antwoord? Klik rechts..!
donderdag 21 oktober 2010
|
|
home |
vandaag |
bijzonder |
gastenboek |
statistieken |
wie is wie? |
verhalen |
colofon
©2001-2024 WisFaq - versie 3
|
Re: Vierkant en driehoeken