WisFaq!

Re: Productie gereedschap

Hartelijk bedankt voor uw snelle en uitgebreide reactie. Hier kan ik echt wat mee.
Ik zat met hetzelfde probleem. Ik wist niet zo goed wat ik met de andere klanten moest, juist omdat de vraag onbeperkt is. Het is me al een stuk duidelijker geworden.
Nu heb ik de volgende vragen opgelost. Zou u met me mee willen kijken of ik dat op een juiste manier heb gedaan?

1. Hoe verandert de optimale oplossing als de kosten om 1000 stuks gereedschap te maken in Amersfoort en deze naar de klant 1 te transporteren 70 euro zouden bedragen.

Kosten worden 70 euro. Opbrengst wordt dan 130 euro. Amersfoort kiest alsnog voor klant 1. Totale winst wordt dan W=130x+80y. Klopt dit?


2. Als de kosten voor het inhuren van extra arbeid 4 euro zijn, zou Hamersma dan extra krachten inhuren?

Amersfoort: 4x200=800 euro extra kosten per 1000 stuks. Winst per 1000 stuks is 140 euro, dus het heeft geen zin.
Breda: 4x300=1200 euro extra kosten per 1000 stuks. Winst per 1000 stuks is 80 euro, dus het heeft geen zin. Klopt dit?


3. Er is een offerte voor het uitbreiden van de productiecapaciteit in Amersfoort met 5000 stuks. De kosten hiervoor zijn 400 euro. Is het verstandig om dit te doen?

5000 stuks: winst = 140 x 5 = 700 euro
Kosten zijn 400 euro. Het is dus verstandig, want het levert 300 euro op. Klopt dit?


4. Hamersma kan 5 uur extra kunnen inzetten voor arbeid. Wat wordt de nieuwe winst?

Ik heb geen idee hoe ik dit kan berekenen. Kunt u me helpen?

Anne
15-6-2017

Antwoord

Hallo Anne,

Vraag 1 en 2 heb je volgens mij goed beantwoord. Jouw redenering bij vraag 3 is niet juist. Je vergeet dat je ook arbeidsuren nodig hebt om de extra productiecapaciteit te benutten, en je hebt maar 5500 uren ter beschikking. Dus: als je in Amersfoort meer gaat produceren (x wordt groter), dan kan je in Breda minder produceren (y wordt kleiner) vanwege de randvoorwaarde:

2x+3y$\le$55

Grafisch ziet dit er zo uit:



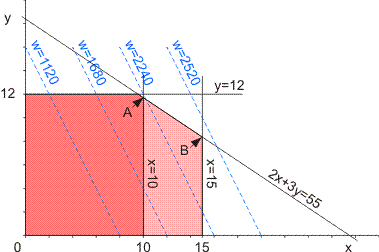
Je ziet de lijnen die de randvoorwaarden weergeven, het donkere gebied is het oorspronkelijke toegestane gebied. Ik heb ook enkele lijnen van gelijke winst getekend (de iso-winstlijnen). Aan de helling hiervan zie je dat punt A het optimum weergeeft (maximale winst).

Wanneer de productiecapaciteit in Amersfoort wordt uitgebreid van 10000 naar 15000 stuks, komt het lichtgekleurde deel bij het toegestane gebied. Het optimum komt nu in punt B. Je weet dan:

x_optimum=15

Invullen in de vergelijking 2x+3y=55 levert je de y-coördinaat van punt B, deze is minder dan de oorspronkelijke 12. Dit betekent: Breda moet minder produceren (door beperkte beschikbaarheid van arbeid).

Met de coördinaten van B kan je de winst berekenen die bij punt B hoort. Waneer deze winst ten opzichte van de oude winst (punt A) meer is toegenomen dan 400 Euro (de kosten voor de investering), dan heeft het zin om de capaciteit uit te breiden. Volgens mij is dit wel het geval.

Dan vraag 4: Hamersma kan 5 uur extra inzetten voor arbeid. Als ik het goed begrijp, verandert de beschikbare arbeid van 5500 uur naar 5505 uur. Dat schiet niet heel veel op, dus ook hier betwijfel ik of dit echt zo bedoeld is. Maar goed, een beetje helpt dit wel. De randvoorwaarde:

200x+300y$\le$5500

verandert in:

200x+300y$\le$5505

De schuin dalende lijn in mijn figuur schuift een klein stukje op, hiermee worden de coördinaten van snijpunten iets anders en vind je een klein beetje extra winst.

Kan je hiermee verder?

GHvD
15-6-2017