F is het voetpunt van de hoogtelijn uit B.
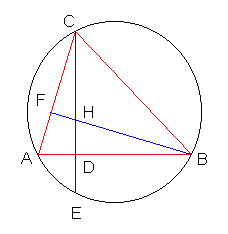
Vanwege de omtrekshoeken is ÐBEC=ÐBAC=a.
Verder is ÐABF=90°-a
Maar ÐDHB=90°-ÐABF=90°-(90°-a)=a
Dit zou verder moeten lukken.
Een vraag bij vraag 2.
Moet er niet bij gegeven zijn dat ÐC scherp is? Anders krijg je negatieve waarden voor ÐP + ÐQ.
Een tip: ÐP = 180°-(ÐB+ÐC)
Bedenk verder dat ÐB+ÐD=180° (vanwege de koordenvierhoek).
succes
Anneke
28-5-2003