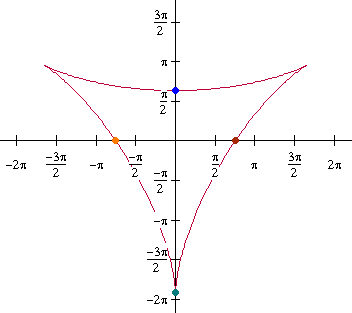
Gegeven voor $t=0..2\pi$:
$x(t)= 4sin(t)+2sin(2t)$
$y(t)= 4cos(t)-2cos(2t)$
Bereken de co÷rdinaten van de snijpunten met de assen.
Uitwerking
$x(t)=0$:
$
\eqalign{
& 4\sin (t) + 2\sin (2t) = 0 \cr
& 4\sin (t) + 2(2\sin (t)\cos (t)) = 0 \cr
& 4\sin (t) + 4\sin (t)\cos (t) = 0 \cr
& \sin (t) + \sin (t)\cos (t) = 0 \cr
& \sin (t)(1 + \cos (t)) = 0 \cr
& \sin (t) = 0 \vee \cos (t) = - 1 \cr
& t = 0 + k \cdot \pi \vee t = \pi + k \cdot 2\pi \cr
& t = 0 \vee t = \pi \cr}
$
t=0 invullen geeft:
$
\left\{ \begin{array}{l}
x(0) = 0 \\
y(0) = 2 \\
\end{array} \right.
$
Snijpunt met de y-as: $(0,2)$
t=$\pi$ invullen geeft:
$
\left\{ \begin{array}{l}
x(\pi ) = 0 \\
y(\pi ) = - 6 \\
\end{array} \right.
$
Snijpunt met de y-as: $(0,-6)$
$y(t)=0$:
$
4\cos (t) - 2\cos (2t) = 0
$
Deze vergelijking laat zich (helaas) niet algebraisch oplossen. Benaderen geeft:
$
t\approx-1,945... \vee t{\rm{ }}\approx1,945...
$
De snijpunten met de $x$-as: $
( - 2,36;0)\,\,en\,\,(2,36;0)
$