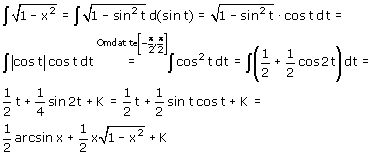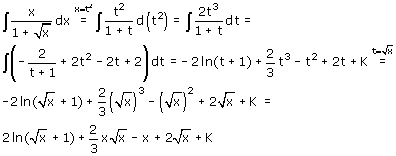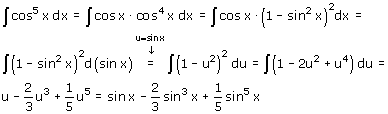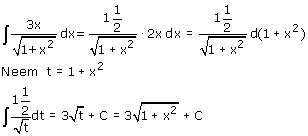|
|
|
\require{AMSmath}



Omgekeerde toepassing
We zoeken $\int{}$f(x)dx
- Kies g(t) zo dat men een primitieve kan bepalen van f(g(t))·g'(t)=h(t)
- Bepaal een primitieve H(t) van h(t).
Er geldt: F(g(t))=H(t)+K, waarbij F een primitieve van f is.
- Als x=g(t) de inverse t=k(x) heeft (alleen dan kan deze methode worden toegepast!) dan is
$\int{}$f(x)dx = H(k(x))+K
We noteren:

Voorbeeld 1
Bepaal $\int{}$√(1-x²)dx op [-1,1]
Stel x=g(t)=sint, t$\in$[-1/2$\pi$,1/2$\pi$]. Dan is t=k(x)=arcsin x.
We krijgen:
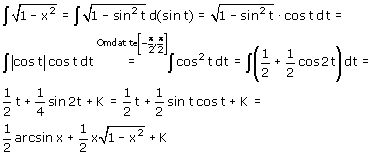
Voorbeeld 2
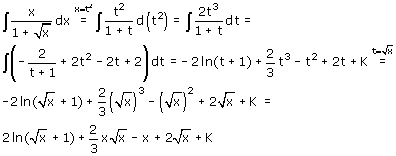
Voorbeeld 3
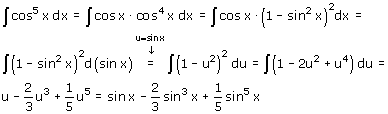
Voorbeeld 4
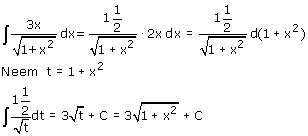



home |
vandaag |
bijzonder |
gastenboek |
statistieken |
wie is wie? |
verhalen |
colofon
©2001-2024 WisFaq - versie 3
|