 De oppervlakte van een ellips kan je berekenen met de formule:
De oppervlakte van een ellips kan je berekenen met de formule:
Opp(ellips) = $\pi\cdot a\cdot b$
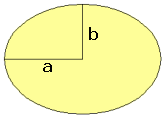
Hierin zijn a en b de 'stralen' van de ellips (zie tekening). Als a=b gaat de formule over in:
Opp(cirkel) = $\pi\cdot r^{2}$
De omtrek is een heel ander verhaal. Er bestaat geen eenvoudige formule om exact de omtrek van een ellips te berekenen. Op MathWorld@Ellipse kan je lezen dat de berekening van de omtrek te maken heeft met elliptische integralen van de tweede soort.
Op de website geven ze ook een manier om de omtrek te benaderen met een reeks:
$\pi \left( {a + b} \right)\sum\limits_{n = 0}^\infty {\left( {\begin{array}{·{20}c}{\frac{1}{2}}\\n\\\end{array}} \right)^2 h^{2n} }$ met $\eqalign{h=\frac{a-b}{a+b}}$
Voor benaderingen van de omtrek kan je de volgende formules gebruiken:
Omtrek $\approx \pi \sqrt {2\left( {a^2 + b^2 } \right)}$
Omtrek $\approx \pi \left[ {3\left( {a + b} \right) - \sqrt {\left( {a + 3b} \right)\left( {3a + b} \right)} } \right]$







 De oppervlakte van een ellips kan je berekenen met de formule:
De oppervlakte van een ellips kan je berekenen met de formule: