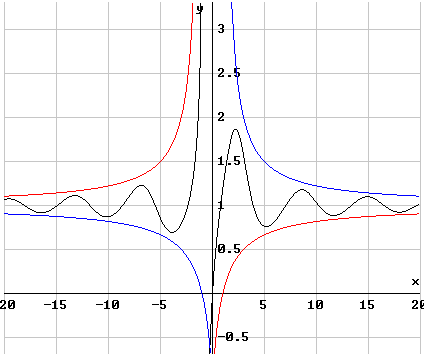
Insluitstelling voor limieten

Stelling

Als $f(x) \leq g(x) \leq h(x)$ en $\mathop {\lim }\limits_{x \to a} f(x) = \mathop {\lim }\limits_{x \to a} h(x) = L$ dan $\mathop {\lim }\limits_{x \to a} g(x) = L$

Voorbeeld

Gevraagd $\eqalign{\mathop {\lim }\limits_{x \to \infty } \frac{{x + \sin x}}{{x + \cos x}} = ?}$

Uitwerking

$
\eqalign{
  & \mathop {\lim }\limits_{x \to \infty } \frac{{x - 1}}
{{x + 1}} \leq \mathop {\lim }\limits_{x \to \infty } \frac{{x + \sin x}}
{{x + \cos x}} \leq \mathop {\lim }\limits_{x \to \infty } \frac{{x + 1}}
{{x - 1}}  \cr
  & 1 \leq \mathop {\lim }\limits_{x \to \infty } \frac{{x + \sin x}}
{{x + \cos x}} \leq 1  \cr
  & \mathop {\lim }\limits_{x \to \infty } \frac{{x + \sin x}}
{{x + \cos x}} = 1 \cr}
$

• bron

F.A.Q.

• Voorbeeld 1
• Voorbeeld 2
• Voorbeeld 3

©2004-2024 WisFaq